本文主要写如何用栈结构来实现简单的计算器，主要包括四则运算，并且在此基础上添加括号、乘方等，示例如下：

$-3.63\times (36.9+26.2)^{5}-5.3*(-2)\div 3.6^{2}.$

下面说说具体如何实现......

1. 内容概述

• 设计用于四则混合运算表达式链栈式存储的数据结构（动态内存开辟，节省资源）
• 创建不同用途的栈，分别用于储存输入表达式的操作数和运算符
• 设计实现浮点数的读取与存储（权值法）
• 为了让计算器能够应对异常的输入，需要设计检查输入的表达式的有效性
• 最后，给出几个测试示例

2. 软件设计

2.1 操作数栈结点的数据结构设计

  由于是链栈式设计，因此一个操作数结点应包含两个部分：信息域、指针域。其中，信息域用一个浮点型数组来存储操作数，指针域则为指向操作数结点的类型指针。如图 1 所示。

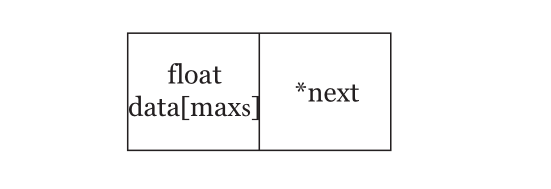图 1：操作数结点示意图

  对于信息域的浮点型数组，操作数的存储可以使用权值表示法。数组的前半部分用来存储操作数的整数部分，后半部分用来存储操作数的小数部分。例如数组$a[6]=\{a_0,a_1,a_2,a_3,a_4,a_5\}$，则该数组存储的操作数实际上是

$\begin{aligned} value=10^2*a_0+10^1*a_1+10^0*a_2+10^{-1}*a_3+10^{-2}*a_4+10^{-3}*a_5.\tag{1} \end{aligned}$

2.2 运算符结点的数据结构设计

  同样的，运算符结点也包含两部分：信息域、指针域。信息域用字符型数据存
储运算符。指针域为指向运算符结点的类型指针。如图 2 所示。

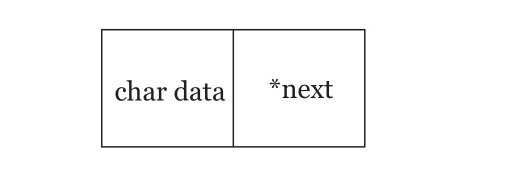图 2：运算符结点示意图

2.3 检查函数的设计

  检查函数主要是检查字符串表达式是否有效，但其检查能力有一定的局限性，该函数的设计有以下几点：

• 该函数对于表达式中连续出现运算符“+”，不认为该表达式无效，而是将其等同为一个“+”；但是对于连续出现运算符“-”则没有相应的操作，认为该表达式无效。
• 该函数可以检查括号是否匹配，括号不匹配包括以下3点：
  • 左括号比右括号数目多
  • 右括号比左括号数目多
  • 左右括号数目相等，但括号内为空
• 于出现四则混合运算符“+、-、*、/”任意两个运算符组合的情况则认为该表达式无效（除了加法运算符连续出现）。

2.4 四则混合运算函数的实现 (主体)

  四则混合运算函数主要包括操作数的读取存储并进行入栈、出栈，运算符的入栈、出栈等操作。

1. 操作数的读取与入栈
   操作数的读取流程如图 3 所示。图中 $s$ 为四则混合运算表达式的字符串，其中读取数字到数组具体过程略去。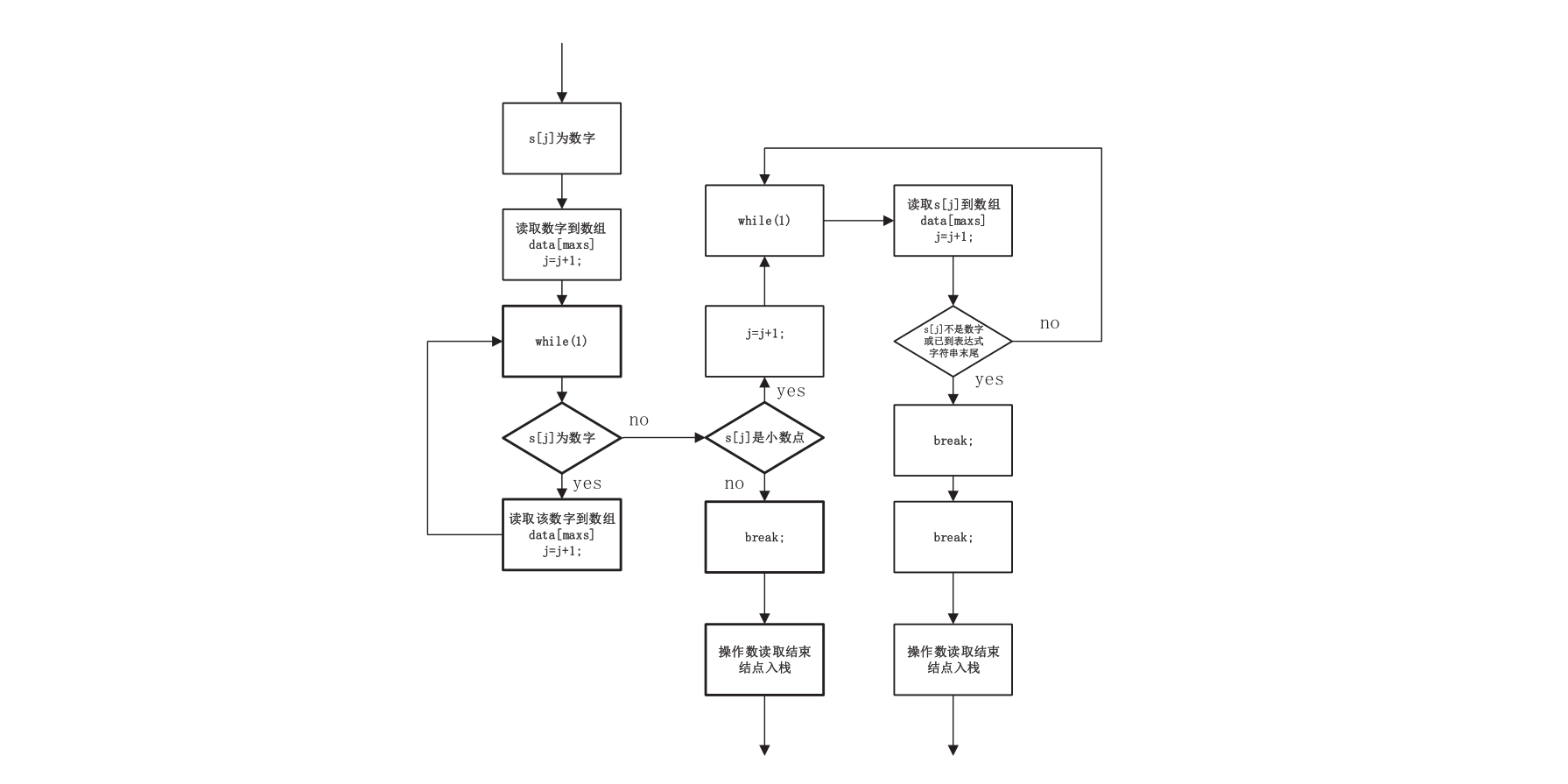 图 3： 操作数读取流程示意图
2. 操作数结点的出栈
   操作数结点出栈时应根据数组的长度及类似式 (1) 确定该数组所代表的操作数。定义数组长度为偶数，则$d[m]$对应的操作数为

   $value=10^{\frac{m}{2}-1}*d[0]+\cdots+10^{0}*d[\frac{m}{2}-1]+10^{-1}*d[\frac{m}{2}]+\cdots+10^{\frac{m}{2}}*d[m-1].$

3. 四则混合运算函数 double cal(string s)

• 计算表达式主要有以下几个思路：
  • 先检查字符串表达式是否有效；
  • 若字符为运算符，则直接入运算符栈；
  • 操作数进栈后再进行判断是否可以进行计算；
  • 加减法不计算，尽管它可以计算（即其后没有更高优先级的运算符）；
  • 对于乘除法，能进行计算的就计算。这包括其后最近的运算符不是括号，也不是乘方运算符等情况（在图 4 中简述为运算）；
  • 进行乘方运算后，若其后最近的运算符不是括号，也不是乘方等运算符；则应考虑其之前的运算符是否有乘除法以进行乘除法运算（在图 4 中简述为运算）；
  • 对于括号，遇到左括号则入栈，当遇到右括号时进行去括号，前述的几点可以保证括号内只有加减运算；去括号的过程中，遇到左括号则该过程结束；结束后应考虑同乘方运算后相类似的情况（在图 4 中简述为运算）；
  • 最终，操作数栈的栈顶元素就是该表达式的计算结果。
• 其他几个特殊的点
  • 在表达式检查完毕后，若表达式有效则将输入参数字符串$s$加上左右括号，这一点主要是为了计算方便。因为在计算过程中，加减法是先不进行计算的，所有优先级更高的如乘、除及乘方计算完成之后再进行加减法计算。加上括号后，在去最外层括号时这些加减法将被计算。
  • 在进行读取操作数或者运算符进栈之前，先将数字0进操作数栈。这一点主要是考虑输入的运算表达式的第一个为运算符“-”或“+”。
  • 为了应对表达式中出现括号内仅有一个负数或带有符号的正数等情况，例如“（-3）、（+4）”，因此在运算符“（”进栈且其下一个字符为“+”或“-”时，先将数字0进操作数栈。
• 四则混合运算函数double cal(string s) 主要实现流程如图 4 所示

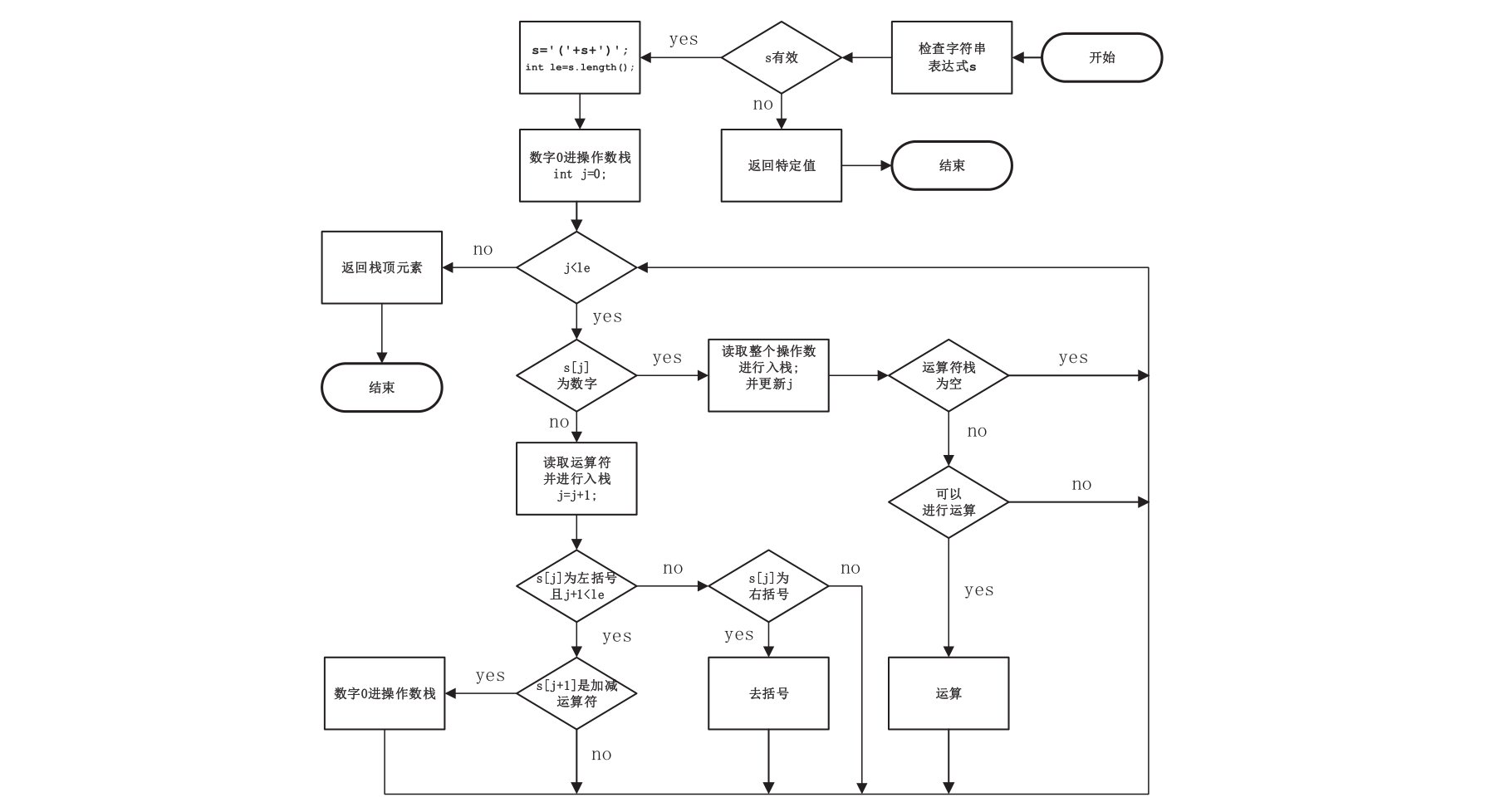图 4：四则混合运算函数 cal 过程示意图

3. 计算示例

3.1 输入表达式有效时运算结果示例

• 首字符为“-”或“+”，以及括号内只有一个数

图 5：软件运行示例结果及验证

• 字符串表达式中有连续的加法运算符

图 6： 软件运行示例结果及验证

图 7：软件运行示例结果及验证

3.2 输入表达式无效时运算结果示例（返回特殊值：3.141592）

• 括号不匹配
  • 左括号数目大于右括号、左括号数目小于右括号、左右括号数目相等但括号内为空等 3 种情况。

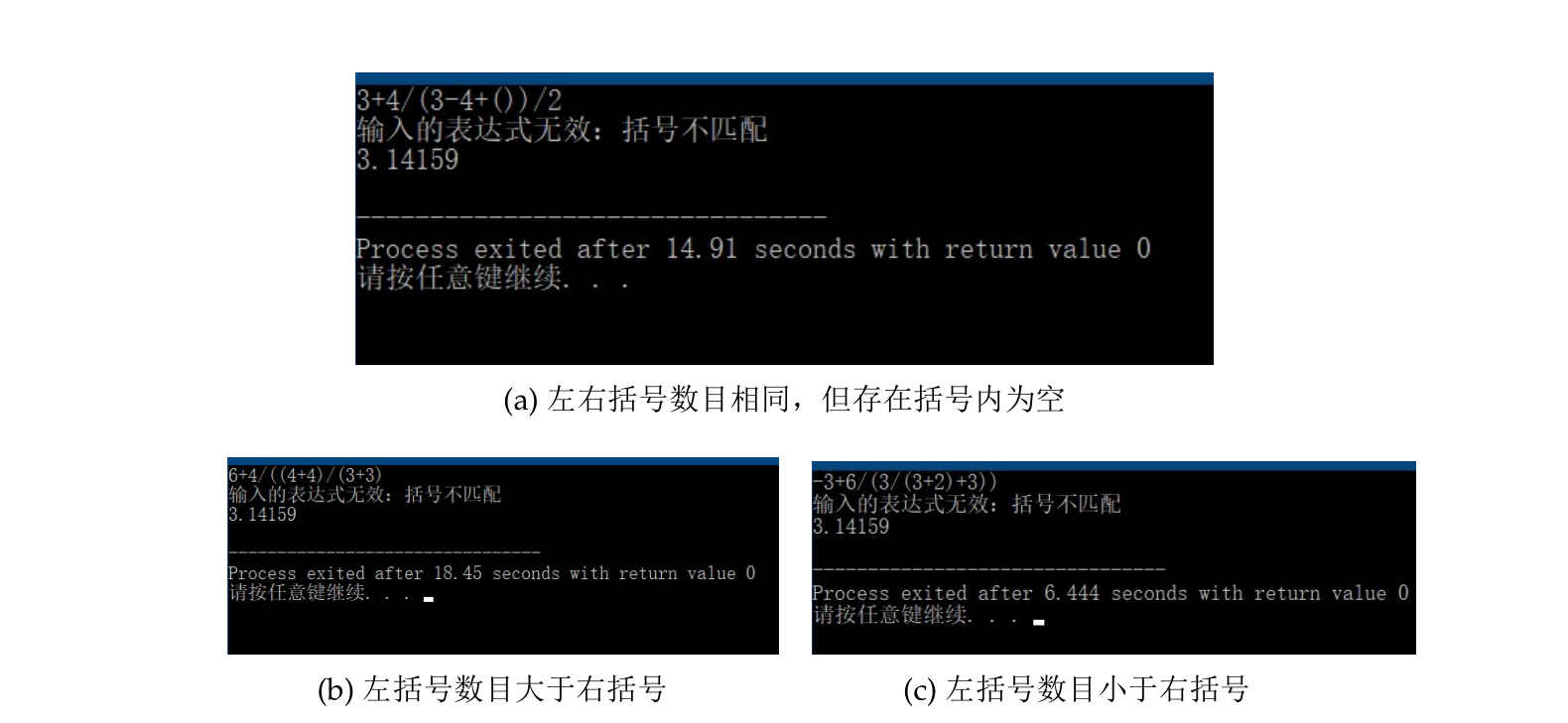图 8：输入表达式无效情况示例

• 字符串表达式中有出现四则混合运算符“+、-、*、/”任意两个运算符组合的情况（加法与加法组合除外）

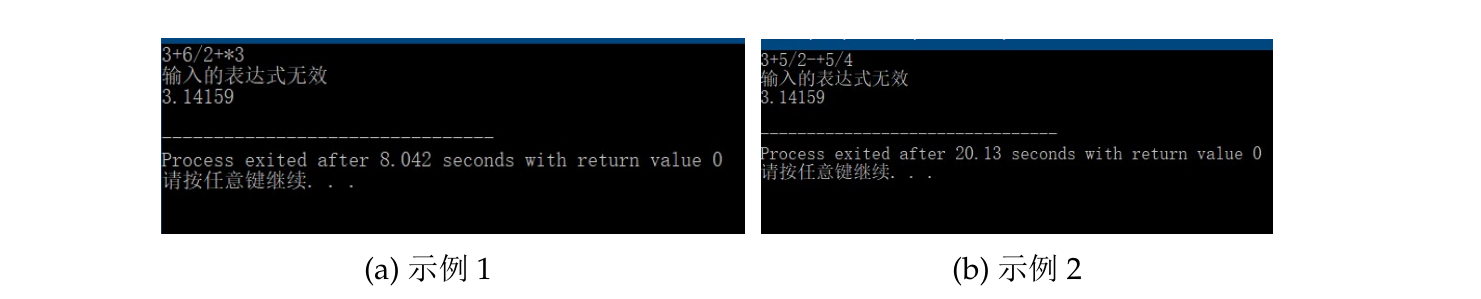图 9：输入表达式无效情况示例

4 软件分析

4.1 性能分析

• 稳定性
  • 软件的设计是根据不同运算符计算时可能遇到的情况，可能有的情况没有想到，就会导致一系列的问题。但就测试情况看来，软件表现的很好。在处理小数，乘除法以及乘方等方面均未发现问题。四则混合运算函数的设计没有进行模块化，看起来可读性较差，如果再其上添加其他运算符或功能会使软件更加冗长。
• 内寸资源利用
  • 软件采用链栈式设计，内存动态开辟，节省内存资源。在进行字符串计算之前先入栈的数字 0 如果没有参加运算在计算结束后会删除该结点，释放内存空间。值得一提的是操作数的存储实际上有点浪费内存空间，存在改进的空间，这一点下面也会说到。
• 处理异常输入的能力
  • 软件设计了检查函数用于检查输入的字符串表达式的有效性。对于一些情况可以进行反馈给用户以改进输入。例如：括号的匹配问题，运算符中间缺少操作数等情况。该检查函数检查有一定的局限性，还有提升的空间，但是难度也不小，因为错误的输入情况远远要多于正确的输入。

4.2 优缺点

• 满意的地方
  • 小数的问题用权值表示法来解决，用数组来存储该操作数。但是有一点可以改进的是可以不用数组来存储而是直接将该操作数计算出来再进行存储，同时这样可以节省很大部分内存空间。
  • 处理首字符为“+”或“-”的情况，先将数字 0 进操作数栈。
• 不满意地方
  • 计算函数 cal 的实现没有模块化，函数体冗长，可读性较差。如果想添加新的运算符或常用函数则会较难。另外软件处理异常输入的能力还有待改进。

5 源代码